On this page:
Simply supported beam P-δ
P-δ is a local effect associated with axial load on displacement relative to element chord extending between end nodes. Figure 1 illustrates the influence of P-δ on a simply supported beam. Here, a longitudinal distributed load ω correlates with elastic bending-stiffness properties KE to induce vertical displacement δ. An additional flexural contribution comes from the relationship between this deformed configuration and axial load P. The geometric stiffness properties KG which dictate this relationship are discussed further in Dr. Edward L. Wilson's text, Static and Dynamic Analysis of Structures.
Values for the maximum flexural response which occurs at element midspan are shown in Figure 1:
Figure 1 - P-δ applied to a simply supported beam
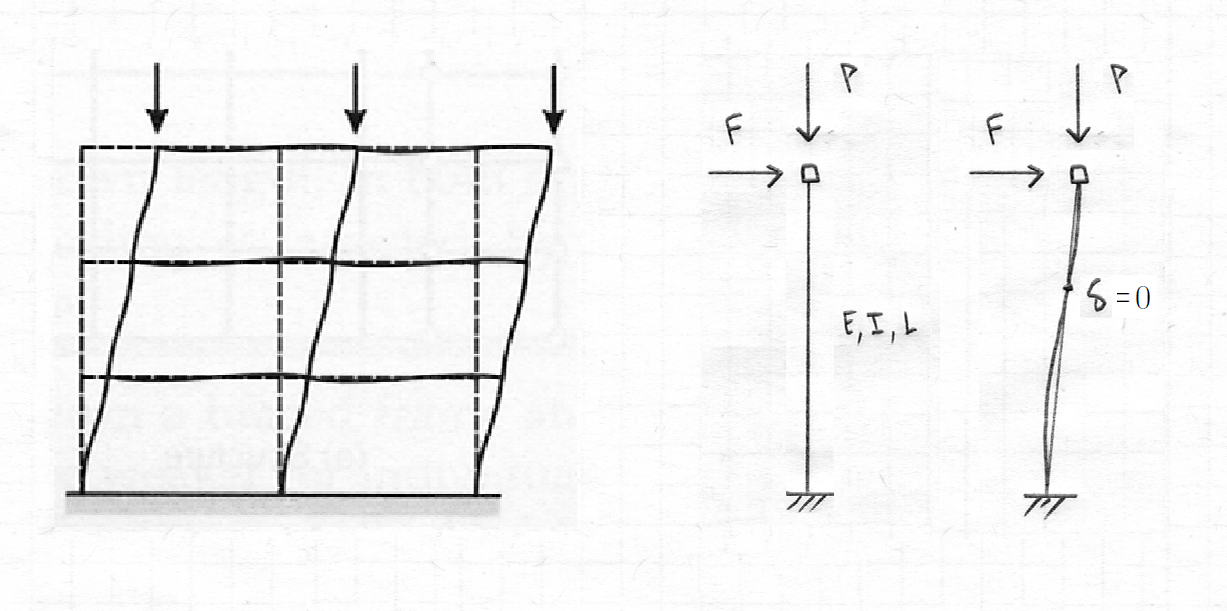
Cantilevered column P-δ
Now, when observing P-δ effect on a cantilevered column, response is shown in Figure 2:
Figure 2 - P-δ applied to a cantilevered column (single curvature)
However, columns seldom displace with single curvature. More commonly, especially with multi-story-building analysis and design, columns deform according to a third-order (cubic) displacement pattern under double curvature. As shown in Figure 3, P-δ effect is much less pronounced because an inflection point intersects the element chord near midspan, previously where displacement from chord was greatest.
Figure 3 - P-δ applied to a cantilevered column (double curvature)
Cantilevered column P-∆
However, what is often of significance, given this loading condition and double-curvature displacement pattern, is P-∆ effect. Although displacement deviates from element chord much less, the lateral displacement associated with story drift is significant. With increasing levels of drift, gravity load has a greater effect on mechanical behavior, as shown in Figure 4. P-∆ effect should be implemented during design, whether static or dynamic, linear or nonlinear.
Figure 4 - P-∆ applied to a cantilevered column
References
- Wilson, E. L. (2004). Static and Dynamic Analysis of Structures (4th ed.). Berkeley, CA: Computers and Structures, Inc.