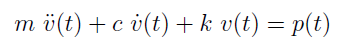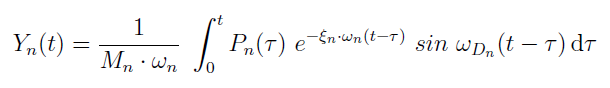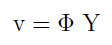To briefly summarize the numerical evaluation of modal analysis, the process for a damped structural system is as follows:
- Mode shapes Φ n, and their corresponding frequencies ω n, are obtained through solution of the following eigenvalue problem:
- Modal damping ratios ξ n are typically assumed from empirical data.
- N coupled equations of motion are given by:
- Their transformation to N uncoupled differential equations is given through the following expression:
- From the previous expression, Y n represents modal amplitude, expressed in the time domain by Duhamel's Integral, which is given as:
- Solution then yields the relationship for total displacement, given as:
where Φ is the N x N mode-shape matrix which transforms the generalized coordinate vector Y into the geometric coordinate vector v.
- Total structural response is then generated by solving each uncoupled modal equation and superposing their displacements. It is advantageous to characterize dynamic response in terms of the displacement time-history vector, v ( t ), because local forces and stresses may then be evaluated directly.
References
- Clough, R., Penzien, J. (2010). Dynamics of Structures (2nd ed.). Berkeley, CA: Computers and Structures, Inc.
Available for purchase on the CSI Products > Books page
- Wilson, E. L. (2004). Static and Dynamic Analysis of Structures (4th ed.). Berkeley, CA: Computers and Structures, Inc.
Available for purchase on the CSI Products > Books page